Today my new preprint with Ali Chamseddine and Alain Connes appeared on “entropy and the spectral action”. In this paper we compute the information theoretic von Neumann entropy of the state associated to the fermionic second quantization of a spectral triple and show that it is given by a spectral action of the spectral triple for a specific universal function. We find a surprising relation between this function and the Riemann zeta function.
In the paper we pass from the one-particle level of spectral triples \((\mathcal A, \mathcal H,D)\) to a fermionic second-quantized level according to the following dictionary:
| algebra \(\mathcal A\) | Semigroup of inner perturbations acting on \(\sigma_t\) |
| Hilbert space \( \mathcal H\) | Clifford algebra \({\rm Cliff}_{\mathbb C}(\mathcal H_{\mathbb R} )\) |
| Self-adjoint operator \(D\) | One-parameter group \(\sigma_t\) of automorphisms on \( {\rm Cliff}_{\mathbb C}(\mathcal H_{\mathbb R} )\) |
There is then a unique KMS\({}_\beta\)-state associated to the \(C^*\)-dynamical system \( ( {\rm Cliff}_{\mathbb C}(\mathcal H_{\mathbb R} ), \sigma_t )\). We show that the von Neumann information theoretic entropy of this state is equal to the spectral action \({\rm Trace}( \mathcal E(e^{-\beta D}))\) where \(\mathcal E(x) = \log (x+1) – \frac {x \log x}{x+1}\) (note that the latter expression is the entropy of the partition of the unit interval in two intervals with ratio of size \(x\)). The function \( \mathcal E(e^{-x})\) looks like:
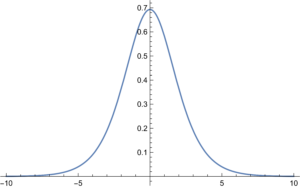
In the second part of the paper we analyze the structure of this function and show that it is a Laplace transform. Hence we can exploit heat kernel techniques that might be available for the heat kernel \({\rm Trace} (e^{-t D^2}) \). We then establish that the coefficients \(\gamma(a)\) of \(t^a\) in an asymptotic heat expansion for the entropy/spectral action are given by \(\gamma(a) = \frac{1-2^{-2a}}{a} \pi^{-a} \xi (2a) \) in terms of the Riemann xi function. We have listed a few of these values below:
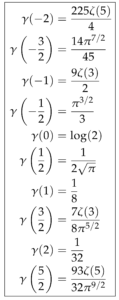
What this table of values also shows is that the functional equation gives a duality between the coefficients of the high energy expansion in even dimension with the coefficients of the low energy expansion in the odd dimensional case.
